一个数反复增减相同的百分比为什么会越来越小

[mostkia]

比如：

初始量为 100，增加 50%再减少 50% = 75

初始量为 100，减少 50%再增加 50% = 75

无论怎么操作，都只会减少，为什么会出现这种反直觉的现象？ 具体到日常生产生活，我感觉这在买基金或者股票的时候会比较明显，有其他需要关注这种问题的领域吗？

[Leonard]

因为增加减少的都是百分比而不是绝对值啊

[VoidChen]

基数不一样

[binux]

你该问问你的直觉。

[mmrx]

这很反直觉么？

[mogita]

今日热点，前排插眼。基数变化了比值能还原？

[Ultraman]

100 * (1+X) * (1-X) = 100 * (1-x^2) < 100 * 1 = 100

[syahd]

x*0.5*1.5 vs x*1.5*0.5
小学五年级的乘法交换律？

[mostkia]

@ck65 @mmrx @binux 具体一些，我想表达的是，为什么无论怎么操作（先增后减，或者先减后增），都只会越来越小？基数变动导致计算后总数不一致，这是可以理解的。

[MozzieW]

x * 1.5 * 0.5 = x * (1.5 * 0.5) = 0.75x
x * 0.5 * 1.5 = x * (0.5 * 1.5) = 0.75x

乘法结合律没有学过? 九年义务教育漏网之鱼?

[sagaxu]

放寒假了

[dayeye2006199]

这就是传说中的 - 辛辛苦苦几十年，一朝回到解放前；病来如山倒，病去如抽丝。感觉并不是很反直觉

[Vegetable]

问问你朴素的直觉。1 的 25 和 0.75 的 25%相同吗？同样的比例下，减少的比增加回来的多，所以越来越少啊。

[CodeCodeStudy]

你中学数学没学好啊

[JeffGe]

因为 (1 - x)(1 + x) = (1 + x)(1 - x) = 1 - x^2 ≤ 1
等号当且仅当 x = 0 成立

[glfpes]

0<x<1, A != 0

==>

|A|(1-x)(1+x)=A(1-x^2) < |A|

[sevenzhou1218]

2333，让我想到了油价，反复涨跌，最后越来越高

[mostkia]

哈哈哈，可能我描述的有问题，我不是说这个结果很奇怪，只是单纯讨论这种现象，看到有人贴出了小学的知识点，好吧，是我没学好，可能当时上课在睡觉吧[doge]。

[mostkia]

我开贴也主要时觉得这种现象在现实中的情况比较值得讨论，比如在买基金和股票时。

[acthtml]

- -！

[HeyWeGo]

这个问题，我觉得特别好！

因为印象里有一个印象特别深的数学题就和楼主提的这个问题有关！
当时上初一，一次平时的数学小测验，有个填空题，内容大概是：有个商家，原价 100 元，先打 5 折卖，然后涨 50%，问商家最后亏还是赚！
我没记错的话，当时全班一共 40 来个人，一共只有 2-3 个人做对了。如果不认真算或者想一想，这种数学上的直觉不一定是先天就有的，现在想来，也许就是人们说的数感~

我觉得楼上没必要觉得楼主这个问题很傻。

[hoyixi]

如果只说奇怪之处，倒是常见，比如物价涨了，10 块涨到 20，然后跌了 5 块变 15，就可以声称物价降幅达 25%

[IGJacklove]

楼上的回答就像"苹果当然会掉地上,难道还飞上天吗?",楼主想知道的是为什么.

[mogita]

@mostkia #8 没想到有生之年能看到一个刻舟求剑的活例子。

[feelapi]

心理学上的“锚定效应”，这里锚定的就是基数，如果基数一直是最开始的数值，那想不明白很正常。

[walsh]

每次增减的基数不同啊

[aydd2004]

这就是老话说的 老天爷不赏你这碗饭吃

[HeyWeGo]

最近我自己也在教小朋友数学。一些成人觉得是直觉的东西，小朋友真的不一定能理解，或者思考的维度不同！

比如我说：“数字 19 后面一个数字是几？”（还是小朋友，只学了 0 和自然数，这是前提）.
平时的时候，小朋友自己能从 0 写到 99，顺序不错，但是我这么问，他就反应不过来。因为在成人看来，我说的后面一个数已经约定俗成了是“比 19 大 1 的数字“也就是”20“，但如果你不把这个约定说出来，小朋友可能想的就是其它数字，因为如果回答”30“，确实也算是 19 后面的一个数字。

回想起来，口语表述中确实有不严谨的地方~

[kaiki]

这是两个不同的动作，你为什么要把第二个动作产生的值和第一个动作的初始值作对比？他们有什么关联吗？
我和王思聪身上都一分钱没有，分别让爹给发了零花钱，我可以买一个面包，他可以买一个面包店还有多的，请问这和我和王思聪身上都一分钱没有的状态有什么必要的联系吗？
扯远了，实际上你把两个式子换成加算就能看出问题了：
100+50-75
100-50+25
第二次计算是基于第一次计算的结果的，你可以理解为：
初始量为 100，增加 50%，100+100*50%，然后减少 50%，(100+100*50%)*50%，连起来(100+100*50%
)-(100+100*50%)*50%
简化
=100+50-(100+50)*50%
=100+50-150*50%
=100+50-75
=100-25
初始量为 100，减少 50%，100-100*50%，然后增加 50%，(100-100*50%)*50%，连起来(100-100*50%
)+(100-100*50%)*50%
简化
=100-50+(100-50)*50%
=100-50+50*50%
=100-50+25
=100-25

你的规则是放大和缩小，那第二次的计算也会因为你第一次的结果放大和缩小而放大和缩小
我在上面列出的计算式中，100 从头到尾都没有发生变化，并不是反复增减相同百分比而变小，而是他要进行计算的都过程是相同的。

[mostkia]

@kaiki 谢谢，打了那么多字来解释，其实计算结果我并不是很关心，因为会算数基本都能都反应过来，只是觉得这种现象本身挺神奇的，这个过程是单向的，只会越来越少，不会多起来，从而联想到现实生活中的影响，发个贴和 v 友讨论一下，没想到大家反响挺激烈的。忽然发现可能因为自己描述的不够好，变成了个奇怪的蠢问题，导致歪楼了😂。
@HeyWeGo 见笑了

[crazytree]

但凡上过课，也不至于问这样的问题

[busymilk]

很难理解么。。。。T﹏T

[kaiki]

@mostkia 其实你这个发现大概就像 0 除以任何不为 0 的数都得 0 一样，只看了一半，没有发现式子本身计算的内容是相同的，0 分成多少分都一样，100 先变大再变小还是先变小再变大也都一样。
你没有觉得这种情况是必然的，所以就会联想到其他的，如果你已经知道是必然的，比如 0 除以任何不为 0 的数都得 0 这件事，那就不会有那种感觉了。

[SWALLOWW]

我也觉得反直觉。。。

可以换个角度理解。

在股市，
你可以用初始本金挣无限多的钱。
然而，如果你亏，却最多只亏一个本金的钱。

股市处于零和博弈，也就是说有人挣钱也有人亏钱。

样本足够大的话大家都处于正态分布状态。
处于一直挣钱的人很少很少，处于一直亏钱的人也很少很少，时赚时亏的人占了很多很多。
但是亏钱最多亏了本金，是有下限，而挣钱的人是没有上限的。

综合，

挣钱的人的钱来自于一直亏的人和时赚时亏的人

所以时赚时亏的人必然也是亏钱状态

有点绕但很现实。

[xiaoyang7545]

你想一下。每次增完是不是 基数会变大。减完基数会变小。

增以减的结果为基数，减以增的结果为基数。那数字自然是会变小。

[zhaol]

一堆人在教别人数学,实际别人问的是心理学.

[acmore]

一个在把基数往大的方向挪
一个在把基数往小的方向挪

[yyyyfan]

感觉是心理直觉，我思考了两分钟，结果就是
钱多了亏得多
钱少了挣得少

[dddd1919]

三个人去投宿，服务生说要 30 元，每个人就各出了 10 元，凑成 30 元．后来老板说今天特价，只要 25 元，于是叫服务生把 5 元拿去退还给他们．服务生想自己暗藏 2 元起来，于是把剩下的 3 元还给他们，那三个人每人拿回 1 元． 10-1=9，表示每人只出了 9 元投宿． 9 乘以 3+服务生的 2 元=29.那么剩下的 1 元呢

同理加减法，比 lz 的乘除法还低级，看看算数达人秒解一下

[LemonK]

@dddd1919 每人出 9 一共 27，服务生收 2 元剩下 25 元给老板。
多老的问题了这是。

[IGJacklove]

@dddd1919 你这逻辑就有问题和楼主不是一回事吧。不是 9x3-2 吗？你 9x3+2 是什么值？？？？

[wudaye]

没想到能在 v 站看到这样的问题。。。

[zepto]

一个股票从 100 跌到 50 只需要 5 个左右的跌停；再从 50 涨回 100 却需要 10 个涨停

[mostkia]

@zepto 是啊，关于这种现象，除了过年商店打折，以及小学应用题里面出现，最近影响到我的就属买基金了，感觉金融上面影响更大一些，感觉挺有意思的，所以开楼讨论一下，没想到歪楼了。。😂我讨论的是这现象本身在生活中的例子以及产生的影响，结果一帮人都开始教我做算数，不过不管是什么评论，都是一种独立的看法吧，我都乐意看到，没人讨论才尴尬。

[ksedz]

想起同事说股票，先涨停再跌停就亏了，先跌停再涨停还是亏

[HeyWeGo]

还是想多回复一条李永乐的视频：《会骗人的数字》

www.youtube.com/watch?v=Ljvlby3yZFQ

[KouShuiYu]

0.5 * 1.5 = 0.75

[misdake]

现实中指数对数的应用还是太少了吧，日常和实业都很难做到指数增长，很难形成相符合的直觉。
也许人类的脑袋能超越加减法，而对乘法有直觉已经很 nb 了。

[KouShuiYu]

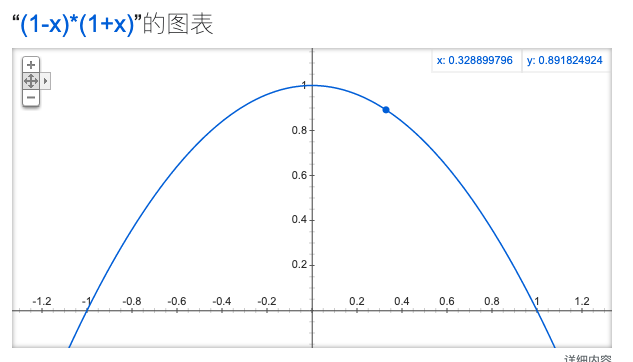[]( https://imgchr.com/i/sLnDsI)不管怎么着都是小于 1

[FrreYin]

@mostkia #43 问题就在于你以为股市真的是按照百分比去涨跌的了，其实并不是

[hello2060]

这个，楼主说反直觉。

难道直觉是，增减同样百分比后回到原数字？任何人都不会有这种直觉吧。

[Jie0zero]

我觉得 6 楼的解答就很精髓易懂哈哈哈

100 * (1+X) * (1-X) = 100 * (1-x^2)

只要 x 大于 0，结果都是比 100 小的

[nznd]

@zepto #42 反直觉的来了 涨停和跌停差距没有 5 个这么大，只有一个的差距，以 100 与 50 举例： 从 100 跌到 50 以下需要 7 个 100*0.9**7=47.8，6 个跌停是 53.14 ，从 47.8 涨到 100 需要 8 个涨停 47.8*1.1**8=102.46 ，从 53 涨到 100 需要 7 个 53.*1.1**7=103.3 （以上计算按心情四舍五入）

[ipwx]

我觉得楼主说得对。

楼上诸君，在形式化之前，这个问题确实很反“直觉”呀？如果你们不是看着下面的式子：

a * (1-x) * (1+x) = a * (1+x) * (1-x) = a * (1 - x**2) < a

你们会觉得这个符合直觉嘛？

类似的还有三门问题，至今还有不少 v2 程序员觉得三门问题的正确答案是错的吧？（ lol ）

====

引申一下，这就是为什么要有数学来形式化的原因，这就是为啥有概率论 => 测度论、几何 => 代数几何 => 黎曼几何，这种东西的原因了。数学本质上就是反直觉的，只不过形式化的东西接触的多了，才慢慢地把一部分反直觉训练成了直觉，然后最后又接触到了新的反直觉了。

[naix1573]

@zepto #42 能不能别说跌，那叫技术性调整，555...

[kop1989]

在善意的前提下，很少有连续百分比的表述。就是为了规避基准的混淆。
人们往往把比例之前的数字当成是基准。
但真实的连续百分比，其实基准是不断变化的。

但恶意情况下屡屡出现。这样的例子有很多。
比如很多贷款、分期都会说“月服务费 x%”。
看起来很少，而且每月是固定的数字。

但你缕清思路之后，总体计算，年息非常可怕。

[gouflv]

在数学工具没普及之前，大部分人就是靠直觉，所以直觉该反就得反

[xJogger]

因为减 50%时，首先减了本金的 50%，这一项就和之前增长的相同了，之后再减利润的 50%，就亏了。

[shintendo]

我觉得上面都没有回答楼主的问题。

“加”使数值变大，因此使后续其它操作的效果放大
“减”使数值变小，因此使后续其它操作的效果缩小

[chniccs]

这题发快手必火

[ward56]

你玩过英雄联盟或王者荣耀吗？ 那个胜率就是场次越多比例越明显，很容易看出一个人的水平，所以一般百场的 70 以上胜率，千场的 60 以上胜率，3000 签以上的 45 胜率就很高啦。
基数愈大，比例越是不作为参考，你滴，明白？

[ward56]

@shintendo 你说反了吧，基数越加，效果越小，基数越减，效果越大。

[lakehylia]

其实就是给你一段绳子，圈一段长方形的地，怎样圈使得圈的面积最大。人的直觉是 1+50%-50% == 1，这就是一维思维，但是实际上面积是 1*(1+50%)*(1-50%) <= 1 。一维空间生活的人类，怎么可能理解二位空间呢~~

[no1xsyzy]

@SWALLOWW “如果你亏，却最多只亏一个本金的钱。” —— 你不会加杠杆（

[shyrock]

这个问题的根本在于，lz 有意无意间把‘增减百分比’理解为加减运算，而实际上，‘增减百分比’是如假包换的乘除运算。
减少 50%就是除以 2，增加 50%只是乘以 1.5 。两者方向相反而系数一大一小，自然算出来的数列就单向递减了。
真正的‘反复增减相同的百分比’应该是‘减少 50%’（除以 2 ）和‘增加 100%’（乘以 2 ），这样的运算结果就会保持不变。

[oamu]

加个限定词吧，一个正数。

[winglight2016]

这个是一种心理现象，叫做“XXX”，抱歉忘记名字了，大意就是大脑倾向于使用现有的数字快速得出结论。比如，笔和橡皮总共 1.1 元，其中笔要比橡皮贵 1 元，问笔和橡皮分别是多少钱？ lz 的问题是类似的，明明是乘法题，大脑却倾向用加减法直接得到正负抵消的结论。

[zlllllei]

@HeyWeGo 这个题感觉像个脑经急转弯， 打五折是按原价打五折，还是按售价打五折？生活经验来看，一般都是按售价打折，而售价未知，只知道最后是按售价的 75 折卖了。

[juncat]

@winglight2016 让我想起了之前看到的一个段子：客人点了个 8 寸的披萨，服务员说 8 寸的没有了，给你们两个 4 寸的可以吗？

[red2dog]

0.5 * 1.5 = 0.75 。 文字上的误导

[ShannonLee]

加减法是互逆运算，乘除法也是互逆运算。 往往互逆运算给人感觉是回到原点。事实上数论里对这种互逆操作后回到原点的准确描述是：实数的加法运算（减法可以看成加这个数的负数（逆元））、去除 0 的实数的乘法运算（除法看成乘这个数的倒数（逆元））构成阿贝尔群，满足交换律和结合律。 产生楼主这样的错觉的原因是：“增减” 听起来像是互逆运算， 而实际上，则这个增减操作同时蕴含了加法和乘法，这个操作无法构成群运算，这样的互逆运算也无回到原点。

所以简而言之就是：（互逆运算给人能回到原点的感觉）&（增减百分比听起来像互逆运算）＝增减百分比给人感觉应该会回到原点。

[ShannonLee]

加减法是互逆运算，乘除法也是互逆运算。 往往互逆运算给人感觉是回到原点，实际上只有满足特定条件的互逆运算才会回到原点。事实上数论里对这种互逆操作后回到原点的准确描述是：实数的加法运算（减法可以看成加这个数的负数（逆元））、去除 0 的实数的乘法运算（除法看成乘这个数的倒数（逆元））构成阿贝尔群，满足交换律和结合律。 产生楼主这样的错觉的原因是：“增减” 听起来像是互逆运算， 而实际上，则这个增减操作同时蕴含了加法和乘法，这个操作无法构成群运算，这样的互逆运算也无回到原点。

所以简而言之就是：（互逆运算给人能回到原点的感觉）&（增减百分比听起来像互逆运算）＝增减百分比给人感觉应该会回到原点。

[nekochyan]

就像上面说的，减 50%是乘以 0.5 倍，也就是除以 2，而增加 50%是乘以 1.5，0.5 跟 1.5 算不上互逆

[q9OxQg]

擦，这不就是说世界怎么折腾都在变糟嘛！躺平算了。

[CodeEncryption]

@ward56 这大小还是看加的是啥吧，按百分比加的话数越大效果越强，按固定值加数越小效果越强

[chenchangjv]

对于相邻的两次增减，前一次增加的绝对值一定比后一次减少的绝对值小。
如果连续增减的开头是增加，那么每两次增减必定减小。
如果连续增减的开头是减少，那么每 2n+1 次增减后必定减小。

[leexy]

数学老师就是这么教的

[jasonkayzk]

这几天也发现了这个问题。股票先涨后跌、和先跌后涨结果都是亏。醉了；

[RRRoger]

我觉得这是一个好问题啊，为什么这么多人秀优越。

楼主是基于向量的乘积有了思维定势吧。

[nomemo]

@ipwx 我觉得你这个算式是最说明白了楼主的疑问

[sgissb1]

我读书的时候，一直也有这个疑问，因为直觉中认为，增加 50%，在减少 50%，不管先后顺序如何，都应该是保持不变的。

但事实上这是个直觉上的错误，因为在直觉的认知中，我们忽略了乘法计算的影响，过多的考虑了加减法。后来我为了扭转我自己的直觉，我每次都会在心算过程中做一些变换。

初始量为 100，增加 50%再减少 50% 变化成计算步骤为：100 * 1.5 * 0.5，基数不变，先乘小数即：100 * (1.5*0.5)
初始量为 100，减少 50%再增加 50% 变化成计算步骤为：100 * 0.5 * 1.5，基数不变，先乘小数即：100 * (0.5*1.5)

由于乘法交换律，可知两种算法结果差不多。或者可目测最终得出的结果大小有括号内结果影响。
所以就用这种办法，避开认认真真计算数，但又相对懒惰的方式在主观上比大小（说是主观，是因为我到这一步的时候，一般不会认真去算结果，都是估计差不多就行了。）

[sgissb1]

事实上是主观上把一些学生时代学的简单算术，归结为加减法的结果。

因为小学学数学都是从加减法起步，然后告诉我们一个规律，加多少在减多少，就会回到原点。包括在学乘法的时候，比如说：

100 * 1.5，实际上老师一般有很多种解释方法，其中一种解释方法就是 100 扩大了 0.5 倍（或 50%），这个里就潜意识中在传达这个数被增加了自身的 50%，所以就会自然而然的用单纯的加法去联想了。

算是刻板影响或者经验主义中的一个典型

[GeekJason]

这不就是股票嘛😂

[guokeke]

如果初始量为负数就会增大 (狗头

[guokeke]

我不知道这里反直觉的定义是啥，如果说是用加法的直觉来代入“增大 50%”这种的算我没说。
这就是个乘法问题。你后面的增减百分比 0.5*1.5 如果小于 1 就减小，大于 1 就变大呗
我可能没理解楼主的意思？为啥不用 0.75 * 1.5 呢？
具体到日常生产生活股票基金，如果没算清就入场叫 “莽夫”，如果没算且不懂还入场叫 “韭菜”，如果被骗子骗了请报警。。

[beijiaoff]

减少 50%就是除以 2，增加 50%只是乘以 1.5 。两者方向相反而系数一大一小，自然算出来的数列就单向递减了。

好问题，上面是好回答

[blank0ken]

@ShannonLee 最满意的回答，很棒

[blank0ken]

看了楼上一些朋友给出的数学工具证明，很棒，但我觉得还是比不上从概念进行逻辑分析来找出漏洞或者说问题的根源来的说服力强，我觉得 @ShannonLee 的回答就是一个很好的回答。就像小学奥数不会讲究提早使用中学甚至大学的数学工具来解决问题（如果用了，会很容易解决），而是会使用各种奇技淫巧从逻辑和概念等别的方法上找到一些解法，因为过早使用强大的数学工具是一种偷懒。

[mzname]

(1+b)(1-b)=1^2-b^2

当且仅当 b=0 时，原值不变

[namelosw]

我上学的时候就觉得这个很反直觉了, 比如买股票, 反复涨跌 3%, 听起来没变实际上赔了.

[shintendo]

@ward56 百分比是确定的，基数越大，数值当然是越大

[alsas]

数死早

[zhjie]

我这么的说吧，什么减一半仓都没啥意思。
看衰全卖，落袋为安。
看好不卖，坚定持有。
行情好，追涨杀跌才赚钱，行情差老老实实余额宝。
基金软件里的涨跌看最近一月 最近三月，有起点价格可以对比涨跌百分比。
昨天+3%今天-3%，那是相比昨天的百分比。
在其它起点来看，这两天百分比不是+3% -3%

[dddd1919]

@IGJacklove 所以真的理解题意了么？纯数学问题在座的所有人用脚也能抠出来答案

[fayetitus]

3/2 的倒数是 2/3，不是 1/2 。
2/3 是无限循环小数，你的单线程直觉在数那无限个六的时候未响应了。

[kaihli]

我換個不是數字的說法。
因為看東西的角度，你以為兩個 50%都是從 150 的角度看，就是 75 。但其實第一個 50%的角度是 100，就是 50 而已。

[linksNoFound]

100/150%*150*=100
50% != 150%

[xianxiaobo]

初始量为 100，增加 50%再减少 50% = 100

初始量为 100，减少 50%再增加 50% = 100

你这样理解就没问题了

[byron]

@chniccs 噗。

[raptor]

我说得更复杂一点吧：

乘法可以通过对数变成加法，所以增加 50%相当于：ln(1.5)=0.4，减少 50%相当于：ln(0.5)=-0.7 。二者本来就不是对称的，所以无论先增后减还是先减后增，结果都是减少

[Anshi]

@ipwx 看了下三门问题， 好有趣啊